Решение задач оптимизации в Excel
Опубликовано: 12.10.2017
Фирма рекламирует свою продукцию с использованием четырех средств: телевизора, радио, газет и рекламных плакатов. Маркетинговые исследования показали, что эти средства приводят к увеличению прибыли соответственно на 10, 5, 7 и 4 доллара в расчете на 1 доллар, затраченный на рекламу. Распределение рекламного бюджета по различным видам рекламы подчинено следующим ограничениям:
а) Полный бюджет составляет 500000 долларов;
b) Следует расходовать не более 40% бюджета на телевидение и не более 20% бюджета на рекламные щиты;
с) Вследствие привлекательности для молодежной части населения различных музыкальных каналов на радио по этой позиции следует расходовать по крайней мере половину того, что планируется на телевидение.
Урок 1.Поиск решения, оптимизация, оптимальный план производства
Необходимо:
1. Сформулировать и решить задачу распределения средств по различным источникам для получения максимальной прибыли от рекламы;
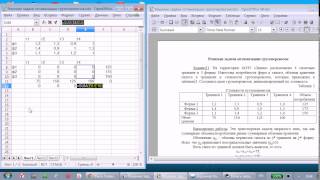
2. Объяснить смысл данных отчета по устойчивости;
3. Определить изменится ли оптимальный план распределения средств, если увеличение прибыли от газетной рекламы снизится до 5 долларов в расчете на 1 доллар, затраченный на рекламу;
4. Определить, в какой вид рекламы будет выгоднее вложить дополнительные средства в случае увеличения бюджета фирмы.
Составим математическую модель задачи, выбрав в качестве переменных
, х4 - количество средств, затраченных на телевидение, рекламные плакаты, радио и газеты соответственно. Тогда ожидаемая прибыль от рекламы может быть подсчитана по формуле (1)Переменные задачи удовлетворяют ограничениям
(2)в левых частях которых вычислены затраты денежных ресурсов на телевидение, радио, газеты и рекламные плакаты, а в правых частях записаны максимально возможные запасы средств на эти ресурсы. Учитывая, что переменные задачи по своему экономическому смыслу не могут принимать отрицательные значения, получаем математическую модель задачи оптимального распределения денежных ресурсов с целью получения максимального дохода от рекламы.